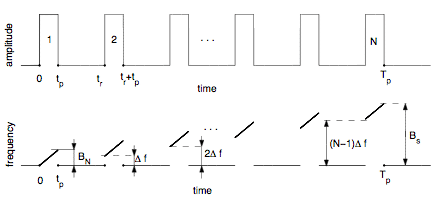
In this project we consider a new family of stepped-frequency waveforms designed for the purposes of high range radar resolution without the expensive hardware needed to support wide instantaneous bandwidth. A stepped-frequency waveform is a collection of short narrowband pulses separated by time intervals that are sufficient to receive scattering echoes from the targets located at some range of interest. Once the echoes from all the pulses have been received, they, then, are processed in the receiver collectively.

The Problem

Traditional stepped-frequency waveforms have some disadvantages. Chief among them is the appearance of relatively high undesirable spikes (range sidelobes and grating lobes) in the profile of the magnitude of the waveform's autocorrelation function.

It turns out that, if both the instantaneous bandwidth and the total processing bandwidth of a radar are known, the right choice of amplitude and number of pulses, as well the magnitude of the frequency shifts between pulses, leads to the reduction of delay sidelobes.

The Solution

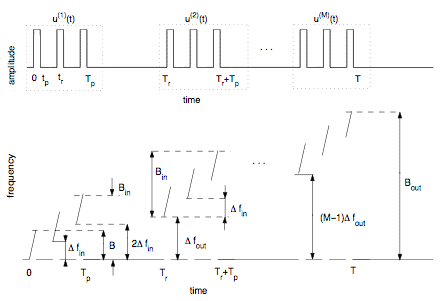
Our solution is based on the usage of variable frequency steps that are introduced by means of specific relationships between the positions of the center frequencies of the pulses. Our approach (which is analytical rather than numerical) advantages from the fact that the ACF of the resulting waveform is available in the closed form. This gives us possibility to search for waveforms with a desired threshold level by analyzing the set of their parameter values. Suitable selection of the parameters allows us to design a variety of LFM trains with excellent ACF profiles

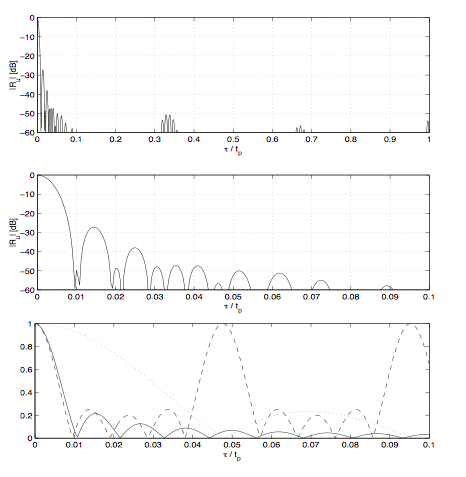
Our analysis shows that it is possible to push the peaks of interest down below the level as low as -50 dB. Below is a sample ACF of such waveform.