AIRS Data Compression (Preliminary Work)
The first part of our work was determining what a good baseline would be for our compression goals. We try to answer the questions: Can the data be compressed and can we improve on current algorithms?
Preliminary Processing
The data contained 51 discontinuous channels (see channel 964 for an example); we assumed that these were so called "radiometric reference channels". Our group performed a simple calculation (the square root of the integral of the squared differences between two adjacent channels) to discover these "bad" channels, and store them separately.
 |
 |
 |
Preliminary Work
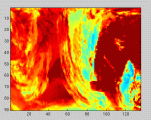
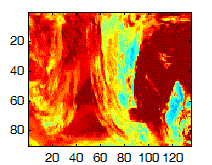
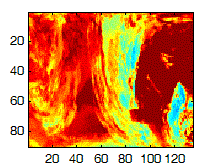
We applied a 2D Discrete Cosine Transform to the original 90x135 image, and noticed that many of the coefficients were negligible (as seen by the blue in the image below).
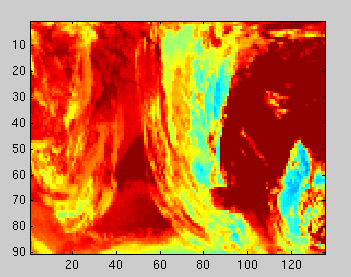 |
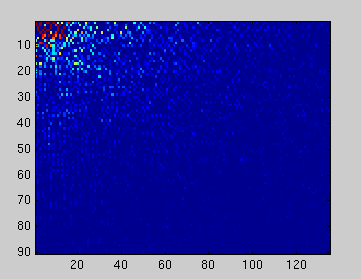 |
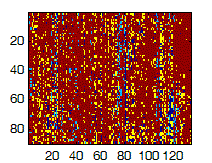
After applying the discrete cosine transform to each 90x135 image in our cube, we looked at the new cube along the channels (Figure 4). Because of the structure of the image, we chose the Haar transform as a preliminary transform.
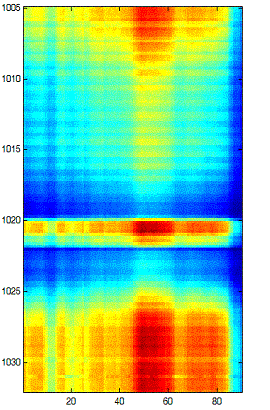 Original Slice |
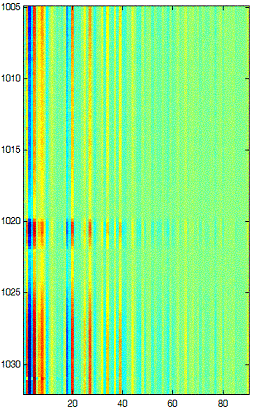 Slice after 2D DCT |
 Slice after Haar |
We then used an adapted Huffman algorithm for coding of the transformed image. Due to project constraints (mostly error correction demands of NASA), our group will focus on fixed-length codes for the final product. However, Huffman is provably optimal (it is a form of entropy coding) and thus serves as a good benchmark for our future work.
Preliminary Results
We achieved a 10:1 preliminary compression ratio (lossy).
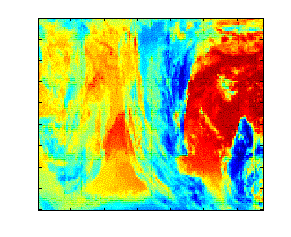
Original
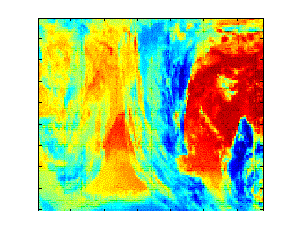
Compressed<->Decompressed
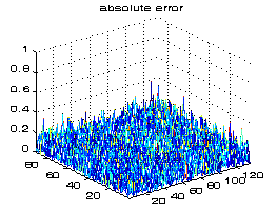
Absolute Error: ± 0.2
 Original |
 Compressed<->Decompressed |
 Absolute Error: ± 0.2 |
|
Ongoing Work
- Adaptive Thresholding: We use a constant threshold to remove the "bad" images. This is not suitable since the range of the data varies from one section of the spectrum to another. The impact of bad channels on the compression ratio is significant. Therefore, we will study more adaptive thresholding techniques.
- Non-separable wavelet transforms: Because of physical properties of the signal, we believe that wavelets will deliver the best transformation of the data (with respect to entropy). Many of current applications of wavelets use so-called "separable wavelet bases" which impose a structure on the plane which is artificial to most images and leads to damage that becomes obvious at the compression ratios demanded by the new hyperspectral instruments.
- Fixed-Length Coding Algorithms: The electromagnetic spectrum is unstable, and, therefore, error correction is a key issue. To minimize the impact of error correction on our compression ratio, we will be looking at non-entropy coding techniques.
- Assembly Programming: The software will reside onboard the real-time satellite system, and, therefore, must be optimized to operate in this environment. The upper bound on the entire procedure is 12 seconds during which time it must process 1 granule (6 minutes or 231.1416 MB of data). For the new GOES-R system, the data rate is 34 times greater. Therefore, some assembly will be written along key execution paths (especially in the advanced mathematical subroutines -- eigenvector calculation, etc).